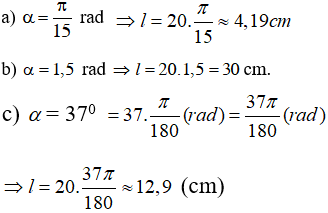Bạn mất khá nhiều thời gian để xác định cung và góc lượng giác trên một hình tròn nhưng vẫn không thể định hướng được. Trong bài viết dưới đây, chúng tôi sẽ chia sẻ kiến thức cung và góc lượng giác chi tiết từ A – Z
Khái niệm cung và góc lượng giác
1. Đường tròn định hướng và cung lượng giác
Đường tròn định hướng là một đường tròn trên đó ta đã chọn một chiều chuyển động gọi là chiều dương, chiều ngược lại là chiều âm. Ta quy ước chọn chiều ngược với chiều quay của kim đồng hồ làm chiều dương.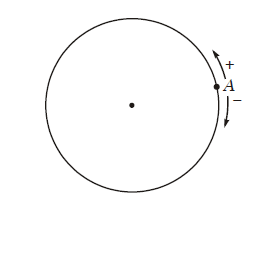
Lưu ý:
- Trên một đường tròn định hướng, lấy hai điểm A và B thì:
- Kí hiệu AB↷ chỉ một cung lượng giác điểm đầu A, điểm cuối B.
2. Góc lượng giác
Trên một đường tròn định hướng, cho một cung lượng giác CD↷. Một điểm M chuyển động trên đường tròn từ C đến D tạo nên cung lượng giác CD↷ nói trên. Khi đó tia OM quay xung quanh gốc O từ vị trí OC tới vị trí OD. Ta nói tia OM tạo ra một góc lượng giác, có tia đầu là OC, tia cuối là OD. Kí hiệu góc lượng giác đó là (OC, OD).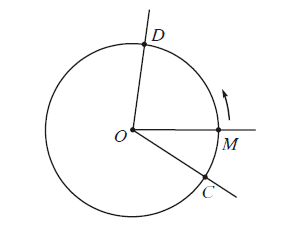
3. Đường tròn lượng giác
Trong mặt phẳng tọa độ Oxy vẽ đường tròn định hướng tâm O bán kính R = 1.
Đường tròn này cắt hai trục tọa độ tại bốn điểm A(1;0),A′(−1;0),B(0;1),B′(0;−1). Ta lấy A(1;0) làm điểm gốc của đường tròn đó.
Đường tròn xác định như trên được gọi là đường tròn lượng giác (gốc A).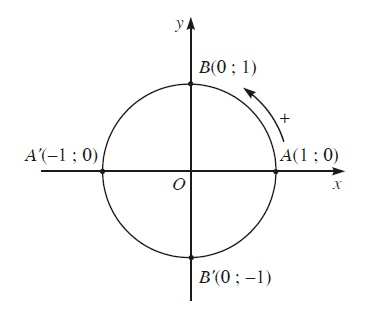
II. Số đo của cung và góc lượng giác
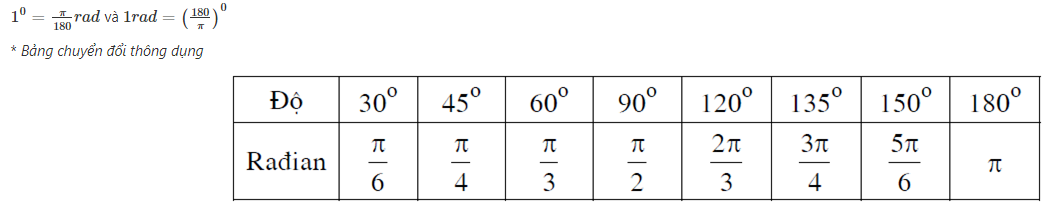
1. Độ và rađian
a) Đơn vị rađian
Trên đường tròn tùy ý, cung có độ dài bằng bán kinh được gọi là cung có số đo 1 rad.
c) Độ dài của một cung tròn
Cung có số đo α rad của đường tròn đường kính R có độ dài
l=Rα
2. Số đo của một cung lượng giác
Số đo của một cung lượng giác AM↷(A≠M) là một số thực, âm hay dương.
Kí hiệu của số đo của cung AM↷ là sđ AM↷.
- sđ AM↷=α+k2π,k∈Z
- sđ AM↷=a0+k3600,k∈Z
3. Số đo của một góc lượng giác
Số đo của góc lượng giác (OA, OC) là số đo của cung lượng giác AC↷ tương ứng.
4. Biểu diễn cung lượng giác trên đường tròn lượng giác
Để biểu diễn cung lượng giác có số đo α trên đường tròn lượng giác, ta chọn điểm A (1; 0) làm điểm đầu của cung vì vậy chỉ cần xác định điểm cuối M trên đường tròn lượng giác sao cho cung AM↷ có sđ AM↷=α.
Bài tập về cung và góc lượng giác
Các bạn có thể tham khảo thêm công thức lượng giác để vận dụng giải các bài tập dưới đây.
Ví dụ 1: Một đường tròn có bán kính 20cm. Tìm độ dài các cung trên đường tròn, có số đo
Từ công thức l = Rα (α có đơn vị là rad) ta có:
Ví dụ 2: Tính sin 25π/4, cos(-240o), tan(-405o).
Lời giải
sin 25π/4 = sin(6π + π/4) = sin π/4 = √2/2
cos(-240° ) = cos(-360° + 120°) = cos 120°= – 1/2
tan(-405o ) = tan(-360o – 45o) = -tan45o = -1
Ví dụ 3: Tìm số đo của các góc lượng giác (OA, OE) và (OA, OP) trên hình 46 (điểm E là điểm chính giữa của cung(A’B’), sđ cung AP = 1/3 sđ cung AB). Viết số đo này theo đơn vị radian và theo đơn vị độ.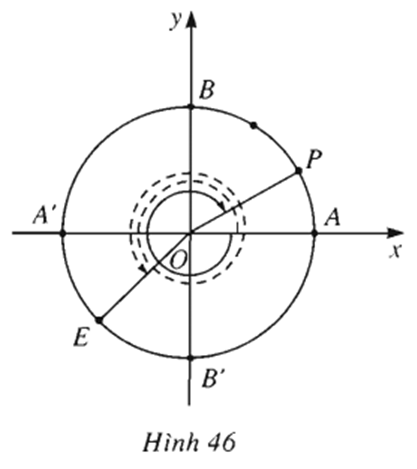
Lời giải:
(OA, OE) = sđ cung(AE)= sđ cung(AB’) + sđ cung(B’E) = – 90o + (-45)o = -135o = -3/4π (rad)
(OA, OP) = sđ cung(AP)= 1/3 sđ cung(AB) = 1/3 . 90° = 30o = π/6 rad.
Hy vọng với những kiến thức về cung và góc lượng giác mà chúng tôi vừa phân tích phía trên có thể giúp bạn nắm được kiến thức vận dụng các các bài tập. Ngoài ra, các bạn có thể tải các dạng bài tập về cung và góc lượng giác trên 123doc chi tiết tại đây.